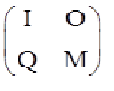ORIGEN
El análisis de Markov, llamado así por los estudios realizados por el ruso Andréi Andréyevich Márkov entre 1906 y 1907, sobre la secuencia de los experimentos conectados en cadena y la necesidad de descubrir matemáticamente los fenómenos físicos. La teoría de Markov se desarrolló en las décadas de 1930 y 1940 por A.N.Kolmagoron, W.Feller, W.Doeblin, P.Levy, J.L.Doob y otros.
El análisis de markov es una forma de analizar el movimiento actual de alguna variable, a fin de pronosticar el movimiento futuro de la misma. Este método ha comenzado a usarse en los últimos años como instrumento de investigaciones de mercadotecnia, para examinar y pronosticar el comportamiento de los clientes desde el punto de vista de su lealtad a una marca y de sus formas de cambio a otras marcas, la aplicación de esta técnica, ya no solo se limita a la mercadotecnia sino que su campo de acción se ha podido aplicar en diversos campos.
Cadenas de markov
Una cadena de Markov, que recibe su nombre del matemático ruso Andrei Markov, es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior. En efecto, las cadenas de este tipo tienen memoria. “Recuerdan” el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Markov de las series de eventos independientes, como tirar una moneda al aire o un dado.
Las probabilidades de transición asociadas a los estados juegan un papel importante en el estudio de las cadenas de Markov. Para describir con más detalles las propiedades de una cadena de Markov es necesario presentar algunos conceptos y definiciones que se refieren a estos estados.
Los estados que pueden sucederse a sí mismos y, además, es posible alcanzar, por lo menos, alguno de los restantes desde ellos se llaman estados transitorios.
Un estado tal que si el proceso entra en él permanecerá indefinidamente en este estado (ya que las probabilidades de pasar a cualquiera de los otros son cero), se dice estado absorbente.
De una cadena de Markov que consta de estados transitorios y absorbentes se dice que es una cadena absorbente de Markov.
Si una cadena de Markov contiene algún estado absorbente, la línea de la matriz de transición correspondiente a las probabilidades de transición de dicho estado constará de un 1 en la diagonal principal y ceros en los demás elementos. Será por lo tanto una matriz no regular.
Estudio de las cadenas de markov
Para poder estudiar las cadenas de Markov absorbentes es preciso reordenar la matriz de transición de forma que las filas correspondientes a los estados absorbentes aparezcan en primer lugar. Así ordenada se dirá que la matriz de transición está en la forma canónica.
Podemos dividir la matriz en forma canónica en cuatro submatrices. La primera es la matriz unidad I, del orden correspondiente. La segunda , la matriz nula. La tercera contiene las probabilidades de paso de estados transitorios a estados absorbentes. La cuarta contiene las probabilidades de estados transitorios a estados transitorios.
Generalizando:
Una cadena de Markov absorbente contiene p estados transitorios y q estados absorbentes. La matriz canónica del proceso presentará el aspecto siguiente:
I: matriz identidad de dimensión q
O: matriz nula de dimensión q x p
Q: matriz de dimensión p x q que contiene las probabilidades de paso de estados transitorios a absorbentes.
M: matriz p x p con las probabilidades de los estados transitorios a estados transitorios.
Se llama matriz fundamental de la cadena de markov a la matriz resultado de la operación:
F= (I-M)-1
Es decir, a una matriz identidad del mismo tamaño de la matriz de transición le restamos esta y posteriormente, hallamos su inversa, que luego nos será de gran ayuda para calcular probabilidades, y detalles que surgen en el análisis de una de esta matrices.
PROCEDIMIENTO DE UNA CADENA DE MÁRKOV
Un proceso de Markov está caracterizado por una función de probabilidad de transición representada por T, llamada matriz de transición, que representa la probabilidades de transito de un estado a otro y un vector de probabilidad de estado inicial que representa el estado inicial del mercado. El procedimiento de la cadena de Markov se detallara a continuación con el ejemplo planteado.
Ejemplo:
La Telefonía móvil de telecomunicación en Colombia: Existen tres operadores: Movistar, Tigo y Comcel.
Vector de estado inicial:
Po = [0,6522; 0,1304; 0,2174]
Matriz de transición:
¿Cómo será la participación en el futuro dentro de 6 meses?
Para estimar la participación de cada uno de los operadores de telefonía dentro de 6 meses lo primero que hay que hacer es multiplicar el vector de estado inicial por la matriz de transición:
Para hallar el valor de T en el periodo 1 se hace lo siguiente:
(0,6522 * 0,6) + (0,1304 * 0,35) + (0,2174 * 0,3) = 0,5015
Para hallar el valor de M en el periodo 1 se hace lo siguiente:
(0,6522 * 0,1) + (0,1304 * 0,4) + (0,2174 * 0,2) = 0,161
Para hallar el valor de C en el periodo 1 se hace lo siguiente:
(0,6522 * 0,3) + (0,1304 * 0,25) + (0,2174 * 0,5) = 0,3275
Entonces se tiene que P1 (Vector de estado en el periodo 1)
P1 = [0,5015; 0,161; 0,3275]
Esta secuencia se hace hasta el P6 cambiando el valor de Po, ya que el estado posterior depende del inmediatamente anterior.
Tenemos P5:
Valor de T en el periodo 6:
(0,4423 * 0,6) + (0,1941 * 0,35) + (0,3626 * 0,3) = 0,4420
Valor de M en el periodo 6:
(0,4423 * 0,1) + (0,1941 * 0,4) + (0,3626 * 0,2) = 0,1943
Valor de C en el periodo 6:
(0,4423 * 0,3) + (0,1941 * 0,25) + (0,3626 * 0,5) = 0,36252
P6 = [0,4420; 0,1943; 0,36252]
La participación en el mercado dentro de 6 meses para Tigo es de 0,4420, para Movistar de 0,1943 y para Comcel de 0,3652. Se puede observar que la participación de Tigo disminuyó, aumentó la de Movistar y Comcel.
Aplicaciones de las cadenas de markov
Se aplica en el posicionamiento de marcas para describir la probabilidad de que un cliente que adquiere la marca A en un periodo, adquiere en su lugar la marca B en el siguiente y analizar la penetración en el mercado.
Se aplica para describir la probabilidad de que una máquina que funciona en un periodo determinado, continúe o falle en el siguiente.
Se aplica en la meteorología si considera el clima de una región a través de distintos días, es claro que el estado actual solo depende del último estado y no de toda la historia en sí, de modo que se pueden usar cadenas de Markov para formular modelos climatológicos básicos.
Otra aplicación son los juegos de azar, un ejemplo es de ruina del jugador, que establece la probabilidad de que una persona que apuesta en un juego de azar termine sin dinero.